
Привет всем! Продолжаю рассказывать о ТРИЗ-педагогике, которая, как песня, нам «строить и жить помогает» . Статьи на эту тему начаты здесь и продолжены тут. Сегодня предлагаю порассуждать на тему: «ТРИЗ-педагогика: зачем делать сложным то, что проще простого?»
- 1. ТРИЗ-педагогика: зачем делать сложным то, что проще простого
- 1.1 Принцип бритвы Оккама
- 1.2 Задача № 237
- 1.3 Озарение
- 1.4 История из 20-х годов
- 1.5 Что советует ТРИЗ-педагогика
- 1.5.1 Вопрос №1, который надо задавать перед решением задачи
- 1.5.2 Вопрос №2, на который надо ответить перед решением задачи
- 1.6 Разбор полётов
- 1.7 По дороге домой

Но лейтмотивом этой статьи будет не бодрячок из кинофильма»Весёлые ребята», а суперхит от Ильи Кормильцева и Вячеслава Бутусова «Казанова» в исполнении группы «Наутилус Помпилиус». Давайте внимательно послушаем:
«А причём здесь ТРИЗ- педагогика?» — спросит меня придирчивый читатель. Вот об этом я и расскажу.
1. ТРИЗ-педагогика: зачем делать сложным то, что проще простого
к содержанию ↑1.1 Принцип бритвы Оккама
В четверг 18 октября 2017 г. перед уроком я поспорил с женой и дочерью. Мы разбирали житейскую ситуацию, которая не имела логического объяснения. Варианты сыпались, как из рога изобилия, но ни одна из выдвинутых версий не объясняла странное поведение нашего знакомого.
Когда поток фантазий на эту тему иссяк, я блеснул эрудицией, и процитировал один из основных постулатов ТРИЗ:
Принцип бритвы Оккама:
«Не умножай сущности сверх необходимого»
(Не надо нагромождать лишнего там, где этого не нужно делать. Объясняй всё просто. Самым простым способом.)

Выдав эту фразу, а следом самое простое и очевидное объяснение проблемы, я с гордо поднятой головой ретировался…
Дорога от двери до двери заняла не более получаса. В 18-00 начался урок.
к содержанию ↑1.2 Задача № 237
Первая задача, которую меня попросил объяснить мой ученик, Дима, была из раздела «Рациональные дроби» из учебника «Алгебры» за 8 класс № 237 с литером «а». Она повергла меня в шок:
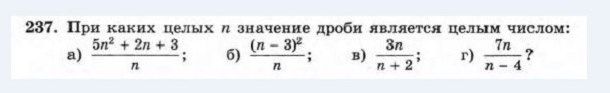
Сначала я обозначил частное от деления в виде некоего натурального числа «а» умноженного на «n»
(a . n). Формула обозначала число, делящееся без остатка на «n».
Делаем преобразования:
5n2 + 2n +3 = n . а . n
5n2 + 2n +3 – an2 = 0
Попытки упростить выражение и алгебраическим путём (через формулы сокращённого умножения) решить это уравнение, ни к чему не привели.
После 15 минут бесплодных метаний в надежде найти другие варианты я пришёл к выводу, что пора воспользоваться одной из старых школьных аксиом:
«Не можешь решить задачу сразу — приступай к следующей. Подсознание продолжит работу и, возможно, в конце концов, подскажет ответ».
Для очистки совести по Вотсапу отправил задачку дочери, закончившей факультет ВМиК (вычислительная математика и кибернетика) МГУ. Шестое чувство подсказывало, что она тоже напряглась.
А эту задачу мы с Димой решили подбором.
Остальные упражнения не вызвали особого труда, но горький осадок от неудачного дебюта остался.
к содержанию ↑1.3 Озарение
После урока по дороге к автобусной остановке на ул. Барклая моё подсознание выдало правильное решение задачи!!!
РЕШЕНИЕ:
Делим числитель на знаменатель «n».
(5n2 + 2n +3) : n = 5n + 2 + 3:n
Теперь анализируем каждое слагаемое отдельно:
«5n» — целый остаток от деления на «n»,
«2» – очевидно тоже целый остаток от деления на «n»,
Последнее соотношение «3:n».
Частное от этого деления может быть целым числом только при «n» равном 1 и 3 или минус 1 и минус 3. Это правильный ответ!!!
В чём была ошибка:
При решении задачи НЕ был принят во внимание один из принципов ТРИЗ:
«Чтобы мыслить функционально, нужно видеть не предметы, а функции».
Я зациклился на том, что задача была из раздела «Рациональные дроби», и пытался решать её формулами сокращённого умножения. От этих шор я отделаться не мог и вместо того, чтобы чётко обозначить цель и искать оптимальное решение задачи, тупо занялся подбором инструментария из указанного раздела.
к содержанию ↑1.4 История из 20-х годов
Молодой делец с Уолл-стрит обратился к Джону Перпонту Моргану. Он послал ему письмо с просьбой о десятиминутной встрече. Письмо мелкого клерка Моргану было не интересно. Он общался только с финансовыми воротилами. Естественно, последовал отказ.

Молодой человек продолжил посылать письма. Он буквально умолял о встрече, уменьшил время с 10 на 5 минут. Это продолжалось 3 месяца, пока не пришло письмо, где было написано:
«Уделите мне 2 минуты. Те 2 минуты, что вы тратите на дорогу от вашего банка до автомобиля».
Такая настойчивость поразила главного финансового туза Уолл-стрит, и он дал согласие.
В назначенный час у дверей банка к Моргану подошёл молодой человек, поприветствовал его, и они пошли дальше. Минуту шли молча.
Морган не выдержал:
— Молодой человек, Вы столько времени просили меня о встрече. В чём дело? Вы идёте и молчите!
— А зачем что-то говорить? Все видели, что мы идём рядом. Теперь любой банк откроет мне кредит!
Вот такой функциональный подход.
Помните: «Вам шашечки или ехать?»
к содержанию ↑1.5 Что советует ТРИЗ-педагогика
к содержанию ↑1.5.1 Вопрос №1, который надо задавать перед решением задачи
«Приступая к решению задачи, сначала задайте себе вопрос: «Для чего? Для чего???»
ПРИМЕР:
Заказчик просит вашу фирму сделать рекламные билборды.
Это совсем не значит, что надо сразу бросаться делать билборды. Задайте сначала Заказчику и себе вопрос: «Вам реклама для чего? Чтобы вас знали или вам щит поставить?»

Всегда есть функция действия. Она будет вашей путеводной звездой при решении задачи.
к содержанию ↑«Смотрите в корень и формулируйте в первую голову то, чего вы хотите достичь. И только потом действуйте!»
1.5.2 Вопрос №2, на который надо ответить перед решением задачи
Для снятия комплексов переименовывайте предметы, с которыми имеете дело, давайте им функциональные названия. (Избавление от шор)
Это правило ТРИЗ звучит так:
«Перед решением задачи замените НЕ функциональное название предмета НА функциональное».
Пример:
Стул — плохо. Сиделка – плохо. Телоудержалка – а вот это уже это хорошее, функциональное название стула.
к содержанию ↑1.6 Разбор полётов
Вернёмся на улицу Барклая.
Выводы:
1) Старый школьный метод: «Не можешь решить задачу сразу — приступай к следующей» — сработал.
Помимо моей воли подсознание продолжило решать задачу и выдало верный ответ.
2) Я был наказан за хвастовство. Сначала бравировал знанием принципа бритвы Оккама:
«Если происходит что-то непонятное, не задавайтесь вопросом: «Почему это происходит?» Задайте себе вопрос: «Как это получить самым простым способом?»
На деле я не смог им воспользоваться. За что и был наказан провидением*.
Примечание:
*Провидение — целесообразное действие Высшего Существа, направленное к наибольшему благу творения вообще, человека и человечества в особенности.
Это ещё раз подтвердило мудрый постулат:
«Знать – это 5% от усвоения истины. ОСОзнать – 95 %»
Как порой это трудно, вы убедились на моём примере.
к содержанию ↑1.7 По дороге домой
На автобусе №2 я ехал домой по Кутузовскому проспекту, а в голове звучала фраза из песни «Казанова» группы «Наутилус Помпилиус» :
«Зачем делать сложным то, что проще простого?..»
Сказано это было совсем по другому поводу…, но суть всё та же.

Сегодня я рассказал вам одну поучительную историю из своей жизни под названием «ТРИЗ-педагогика: зачем делать сложным то, что проще простого». Она лишний раз подтверждает истину, высказанную ещё древними греками, о том, что в этом мире всё связано со всем. Рок-музыка с философией, философия с математикой, математика с ТРИЗ…
В заключение предлагаю послушать ещё один шедевр от любимой группы «Наутилус Помпилиус» — «Одинокая Птица»:
Тут и домашнее задание родилось.
Открытая задача: «Как песня «Одинокая птица» связана с ТРИЗ-педагогикой и математикой?»
Пишите в комментах. До новых встреч на блоге.
С уважением
Автор блога Алексей Фролов



Через философию
Сергей, привет! Через философию — это я понял. А конкретнее, если по полочкам разложить?
Единственное, что мне приходит на ум — это то, что и ТРИЗ-педагогика, и математика и философия требуют от человека развития абстрактного мышления. Песня «Одинокая птица» тоже полна неких образов, из которых слушатель должен сложить цельную картину идеи, которую заложил автор.
Если это не так, то пока не говорите правильный ответ :0)
Сергей, здравствуйте! Головоломка, которую я задал, относится к числу так называемых «открытых задач». В отличие от закрытых задач (пример: 2х2=4) у открытых нечёткие условия, много путей решения и много ответов, из которых несколько правильных. Именно такие такие задачи мы решаем в жизни (пример: Какую машину купить? На ком жениться?…) Цель этих задач — развитие креативности, нестандартного мышления, избавление от шор, которых с годами всё больше.
Но тогда получается, и решение задачи будет чисто субъективным? Т. е. вполне может не совпасть с задуманным Вами?
Конечно, и часто мои ученики дают ответы намного лучшие, чем контрольные (которые были реально использованы в жизни или придуманы специалистами)
Про домашнее задание ничего не поняла, а статью прочитала. Не первый раз у Вас на блоге, статьи интересные, но не для каждого ума. Сейчас я сталкиваюсь с тем, что люди вообще не понимают ни чего, даже самых элементарных вещей. На мой взгляд это происходит от того, что думают только о себе, о своем мироощущении. А чтоб решить проблему того или иного человека, нужно сначала понять, как именно он воспринимает действительность. В большинстве своем люди и живут «зачем делать сложным то, что проще простого» или еще А МЫ НЕ ВНИКАЛИ. Я так поняла, чтоб задачу Вашу решить, надо еще предыдущие статьи прочитать, что то с первого раза не заходит.
Мария, здравствуйте! А я в таких случаях вспоминаю фразу, которая Агата Кристи однажды сказала своей собеседнице: «Дорогая моя! Дело в том, что люди в основном глупы». Это утверждение я отношу и к себе самому. Когда анализируешь свои поступки, порой диву даёшься: «Зачем я это сказал, почему так сделал?»
Как противоядие от глупости я выработал привычку: когда не понимаю, что сказать, — молчу. Это очень ценное качество. Не даром же говорят, что «счастливый брак от несчастного отличается всего несколькими фразами, не высказанными вслух»
Я вообще по натуре человек не очень разговорчивый, стараюсь больше слушать, а высказываюсь только в тех случаях, когда уже молчать нельзя, ну а что касается человеческой глупости, так она в наше время на каждом шагу.
А поняла теперь, песню надо было послушать. Нет такой возможности домашние спят. Но в любом случае спасибо за статью, очень понравилась моментами интересно.
Мария, здравствуйте! Спасибо за теплые слова. Я сейчас увлекся идеей найти точки соприкосновения ТРИЗ и математики, в идеале, и психологии. Первые шаги делаю, публикуя рассказы о своих находках в этой области. По возможности буду продолжать. Тем более моя практическая деятельность постоянно подкидывает новые темы и сюжеты.