Математика 1 класса без ошибок

Привет всем! Как интересно устроена жизнь. Она порой переворачивает всё с ног на голову.   Дело, которым я занимался последние 40 лет в качестве хобби, вдруг стало моим средством для существования. А то, чему учился и посвятил долгие годы, вдруг перестало приносить дивиденты и кануло в лету.

Главное в такой момент, чтобы голова не закружилась. И есть от чего. Эта статья снова о ЗОЖ, о способах выживания в наше не простое время. Называется она, как ни странно, «Математика 1 класса без ошибок».

1. Математика 1 класса

1.1 Два примера из практики

О проблемах обучения математике знают все: и те, у кого есть дети, и те, у кого их нет. Поэтому не буду в сотый раз теоретизировать и повторять то, что уже сто раз сказано, а начну с двух примеров из своей практики:

Пример № 1

Решаем с учеником задачу №10 стр.13 учебника математики для 3 класса, 2 полугодие. Авторы — Б.П. Гейдман и другие.

«Если корове выдавать ежедневно по 6 кг сена, то запаса сена хватит на 14 дней. На сколько дней хватит этого запаса сена, если корове выдавать 7 кг в день?»

 

Решение, которое дал третьеклассник:

“Из 14 дней вычитаем 6 кг, а потом итог умножаем на 7 кг. Ответ: Сена хватит на 56 дней!”

Пример № 2

Задача № 4 стр.14. Учебник тот же.

«Сережа лёг спать в 9 вечера, а проснулся в 7 часов утра следующего дня. Сколько часов спал Сережа?»

 

Вот какое решение было мне предложено:

“9 часов умножаем на 7 часов. Ответ: Сережа спал 63 часа!”

 

1.2 О бравом солдате Швейке

Согласитесь, эти ответы напоминают эпизод из «Похождений бравого солдата Швейка», когда судебная медицинская комиссия проверяла его на сумасшествие:

«…Но один из членов попросил разрешения задать ещё один вопрос:

— Сколько будет, если умножить двенадцать тысяч восемьсот девяносто семь на тринадцать тысяч восемьсот шестьдесят три?

— Семьсот двадцать девять, — не моргнув глазом, ответил Швейк.

— Я думаю, вполне достаточно, — сказал председатель комиссии. — Можете отвести обвиняемого на прежнее место…»

 

Но в нашем случае проблема не в «Швейке», а в преподавателях, которые учат писать и считать, но не учат думать.  А зачем?

До сих пор повсеместно практикуется система преподавания из XVII века:

• Знакомство с новой темой в классе
• Изучение пройденного материала дома
• Пересказ изученного материала в классе. Чем ближе к тексту учебника, тем лучше

Где тут место для собственной мысли и творческого подхода? Скажите на милость!

1.3 Зачем делать сложным, то, что проще простого?

И ещё. Ответьте честно на вопрос: «Сколько раз в жизни вы дифференцировали, совершали действия с логарифмами или интегрировали?» С большой вероятностью ответ будет как у Афони (орфографию не исправляю):

Для справки. Афоня персонаж из одноименного фильма застойных времен.

Поэтому лично я рассматриваю математику, скорее, как инструмент для развития мозга. Этим, собственно, и занимаюсь последние годы.

1.4 Перечень проблем при изучении математики

Перечислю ряд сопутствующих проблем, с которыми я сталкиваюсь при обучении детей математике:

1.4.1 Потеря интереса к математике

Это самая большая проблема. Без ее решения обучение вообще невозможно, т.к. всё будет происходить по сценарию:

«Смотрит в книгу, а видит фигу».

А вот и рисунок. иллюстрирующий это высказывание:

1.4.2 Отсутствие уверенности в своих силах

Этому недугу способствует широко распространенное мнение, что существует какой-то особый (“гуманитарный”) склад ума, который не способен к изучению точных наук. Это заблуждение. Мозги у всех нас одинаковые и с громадным потенциалом нераскрытых возможностей.

1.4.3 Привычка действовать механически, только по заученным алгоритмам

Этому способствует натаскивание для подготовки к ЕГЭ. Недавно услышал термин: «Поколение ЕГЭ» Оно уже выросло и скоро о себе заявит. Когда представитель упомянутого поколения встречает новую задачу, которая не укладывается в «прокрустово ложе» известных вариантов решений, у него опускаются руки. Он впадает в ступор.

1.4.4 Боязнь ошибиться

Английская пословица гласит :

«Нет срывов – нет прорывов». Оригинал: “No Breakdowns – No Break throes”.

Детей надо учить экспериментировать, не страшиться отрицательного результата, уметь уважать и анализировать свои и чужие промахи. От ошибок тоже есть польза. Они показывают, что выбранные решения не верные. Надо искать другие. Многие великие открытия были сделаны после сотен и тысяч неудачных экспериментов.

1.4.5 Привычка спешить

У каждого человека свой темп. Неловкость от того, что кто-то решит быстрее, ограничение времени на решение задания вызывают спешку. торопливость, как правило, приводит к ошибкам. Этим грешат почти все дети.

1.5 Что мы можем всему этому противопоставить?

С чем бороться, мы выяснили. Теперь попытаемся ответить на вечный русский вопрос: «Что делать?»

Мой практический опыт преподавания математики свидетельствует том, что все перечисленные болячки «прусской» системы обучения прекрасно лечатся с помощью методов ТРИЗ-педагогики.

В этом мне помогают пять фундаментальных принципов Педагогической техники([1]):

• «ПРИНЦИП ОБРАТНОЙ СВЯЗИ»,
• «ПРИНЦИП ДЕЙСТВУЙ»,
• «ПРИНЦИП СВОБОДЫ ВЫБОРА»,
• «ПРИНЦИП ОТКРЫТОСТИ»,
• «ПРИНЦИП ИДЕАЛЬНОСТИ»

и соответствующие им приемы:

Разберемся по пунктам.

[1] Из книги А. Гина «Приёмы педагогической техники».

1.5.1 Как избежать потери интереса к математике

1.5.1.1 «Удивляй»

К каждому занятию я готовлю математический фокус. Потом мы все вместе разбираем его секрет, и я предлагаю желающим проделать его самостоятельно.

Пример:

1.5.1.2 Не томи теорией более 15-20 минут за урок

Если материал большой, чтобы не наскучить, целесообразно растянуть его на несколько уроков, а не давать весь сразу. Обязательно после теории надо решить несколько задач на пройденную тему. (ПРИНЦИП ДЕЙСТВУЙ).

Задачам я придаю сказочную или приключенческую форму:

Пример:

«Змей Горыныч и Добрыня Никитич решили выпить квасу. Змей Горыныч выпил в 3 раза больше, чем Добрыня Никитич. Сколько выпил каждый, если вместе они выпили 8 бочек кваса?»

Змей Горыныч и Добрыня Никитич наквасились

В перерывах между математической теорией и практикой «на ура» проходят ТРИЗовские задачки от Кота Потряскина. При их решении можно практиковать и МОЗГОВОЙ ШТУРМ, и устраивать командные соревнования. Урок проходит незаметно и очень весело.

Кот Потряскин

Для более старшего возраста в качестве прокладки между частями урока я применяю открытые задачи из ТРИЗ- литературы. Последнее время дети уже в начале урока спрашивают: «А открытые задачи будут?» После положительного ответа хлопают в ладоши и кричат «ура».

1.5.1.3 Делай физкультминутки

Если я вижу, что ученики устали сидеть на одном месте, я придумываю групповые занятия, что заставляет их встать, походить, переставить мебель.

Можно просто объявлять физкультминутку. Мы с мальчиками отжимаемся от пола на кулаках, как десантники,. Девочки приседают или делают наклоны.

 1.5.1.4 Решай задачи с инспектором Варнике

Ребятам очень нравятся задачи с инспектором Варнике, которые в 60-е годы публиковались в журнале «Наука и жизнь». Они учат быть наблюдательными, отслеживать причинно-следственные связи, выстраивать логические цепочки, дают новые знания из различных областей. За урок решаем 1-2 такие задачи. Если ответ не найден, оставляю интригу до следующего занятия.

Дело о краже из кассы

1.5.1.5 Корректируй план урока в процессе преподавания

Уроки надо готовить, но если в ходе реализации намеченного плана вы видите, что дети заскучали или просят какое-то конкретное задание, надо быть готовым действовать по обстановке. (ПРИНЦИП ОБРАТНОЙ СВЯЗИ и ПРИНЦИП СВОБОДЫ ВЫБОРА)

На такие случаи в арсенале надо всегда держать интригующую информацию, веселые задачки, фокусы и головоломки по разным темам.

1.5.1.6 Отходи от традиционного подхода, когда, строго следуя программе, идут от простого к сложному

Мои эксперименты по обучению первоклашек логарифмам, пропорциям, дробям, процентам дают прекрасные результаты. Возникает вопрос: «Стоит ли ждать 5 лет, чтобы подойти к перечисленным темам?»

Способным и креативным ребятам будет скучно плестись в ногу со стандартной программой. Результат будет тот, против которого мы боремся – потеря мотивации.

Потому вооружившись ПРИНЦИПОМ ОБРАТНОЙ СВЯЗИ надо подходить к процессу обучения индивидуально. Не тормозить передовиков, и не гнать отстающих.

1.5.1.7 Играй в конце урока

К пониманию важности игровых видов обучения я пришел через спорт. Много лет занимался атлетикой, потом аэробикой, бегом. Все наскучило. В конце концов, остановился на большом теннисе.

Чтобы расстояние, которое ты пробегаешь во время игры, преодолеть на беговой дорожке, надо иметь железную волю. В игре это не заметно. Летит мяч — его надо отбить. И не просто отбить, а в зависимости от местоположения партнеров, отбить туда, куда надо. Это шахматы на корте.

«В теннис играют руками, думают головой, а проигрывают ногами»

Работает не только тело, но и серое вещество. О чем ещё мечтать?

Элемент соревновательности очень важен и в обучении. В ТРИЗ-педагогике разработана игра «Креатив-бой», когда в решении открытых задач соревнуются несколько команд.

Нечто похожее мы используем на уроках математики.

1.5.1.7.1 Крестики-нолики

В зависимости от количества учеников в классе игра проходит в виде соревнования команд или отдельных участников.

Пример игры по теме «Возведение в степень»:

Рисуется сетка: по вертикали — показатели степеней, по горизонтали — числа. Цель — построить заданную фигуру из клеток (как в игре “Крестики-нолики”). Но для хода в нужную клетку надо соответствующее ей число возвести в соответствующую этой клетке степень.

При этом решение математической задачи из обузы превращается в удовольствие. Повторное выполнение одной и той же задачи вызывает восторг (быстро можно походить и результат известен), а не унылое: «Мы это уже решали».

Очень хорошо так учить таблице умножения, взяв за базу таблицу Пифагора.

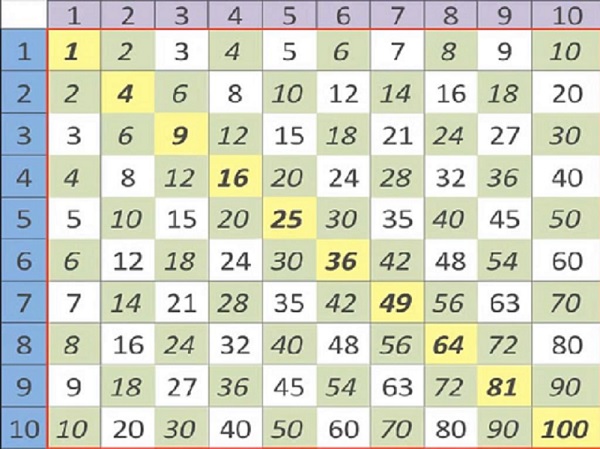
Для зачета хода ученики должны правильно перемножить соответствующие цифры по горизонтали и вертикали.

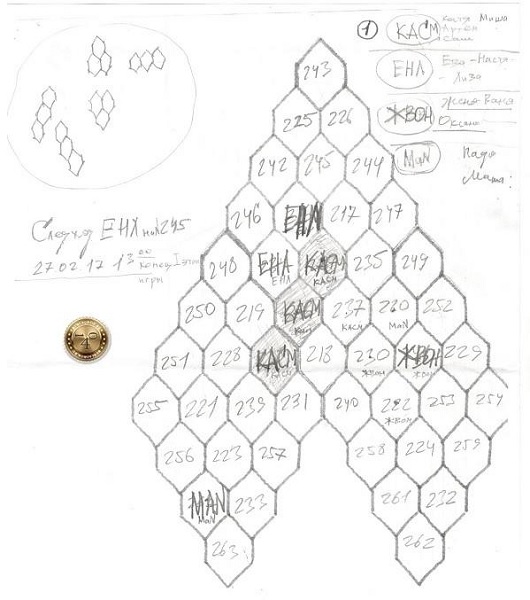
1.5.1.7.2 Виноградная лоза

Другой вариант (на фото ниже), когда каждой клетке присваивается номер задачи. Полем для игры является фигура, похожая на виноградную лозу.

Решил задачу — записал свой значок в клетке. Не решил – пропускаешь ход.

1.5.1.7.3 Шахматы

Отличным средством для творческого развития являются шахматы. Это отдельный урок, но цель его та же. Мы разгадываем шахматные задачи, разбираем партии, изучаем теорию. Здесь простор для творчества колоссальный.

Пример:

Вот один из типов задач, которые нравятся ребятам.

Каждый ход — взятие фигуры. Цель, чтобы на доске осталась только одна фигура. Попробуйте. Задача не лёгкая.

Каждый ход — убийство

1.5.1.7.4 Настольные математические игры

Сейчас выпускается много развивающих игр для детей. Особенной популярностью на моих уроках пользуется игры: с дробями «Делиссимо», на таблицу умножения «Цветариум» и «Много-много» и другие.

1.5.1.8 Связывай материала с жизнью, выходи за рамки изучаемого предмета

Этот тезис полностью соответствует ПРИНЦИПУ ОТКРЫТОСТИ

Для примера возьмем распределительный закон умножения.

Можно просто зазубрить приведенные формулы. Толку от этого будет мало.

А можно после объяснения теории показать область применения этого закона для перемножения больших чисел.

Решить несколько примеров. В этом случае полученные знания станут инструментом на всю оставшуюся жизнь.

Полезно показывать связь математики с другими областями науки и культуры.

Например, при изучении материала о пропорциях уместно вспомнить Леонардо да Винчи

1.5.1.9 Привлекай к процессу обучения родителей

О важности контактов с родителями лишний раз говорить не приходится.

Если родители во время занятия не уходят, а ждут ребенка, можно пригласить их в класс, дать задание, предложить участвовать в групповой игре. Если после урока они возьмут задачи с собой, и дома, в семейном кругу, продолжат их решение, это будет просто замечательно.

1.5.2 Как избавиться от отсутствия уверенности в своих силах, боязни ошибиться, привычки действовать механически, только по заученным алгоритмам

1.5.2.1 Решай ОТКРЫТЫЕ ЗАДАЧИ методом МОЗГОВОГО ШТУРМА

Здесь опять на выручку приходят открытые задачи (ПРИНЦИП ОТКРЫТОСТИ).

При их решении чаще всего используется метод МОЗГОВОГОШТУРМА (МШ)

На первом этапе МШ (Создание банка идей) запрещено критиковать предлагаемые решения и их обосновывать.

При такой постановке вопроса неправильных ответов нет. Это раскрепощает учеников. Позволяет постепенно уйти от закомплексованности и боязни предложить ошибочное решение.

На втором этапе МШ (Анализ идей) из всего многообразия предложенных решений выбираются наиболее эффективные и общими усилиями доводятся до совершенного уровня (ПРИЦИП ИДЕАЛЬНОСТИ)

1.5.2.2 Используй наглядные задачи

Наглядные задачи в чем-то родственны открытым задачам. Этот тип задач значительно превосходит все остальные типы закрытых задач на этапе ознакомления маленьких детей с математикой:

Они не требуют знания русского языка, вникания в смысл текста.

Для разгадки этих задач можно даже не уметь писать. Их решение одновременно служит и их оформлением.

Приучают к графическому изображению условий задачи и их решений.

Часто имеют много вариантов решений, что позволяет ученику проявить свою индивидуальность.

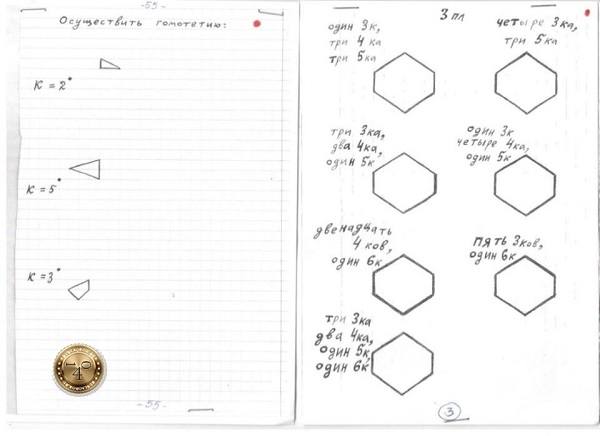
Задачи на разрезание прямыми линии (№3) можно решить, только проведя произвольно заданное количество линии (т.е. через ошибку). Потом надо эту «ошибку» исправлять, начиная перемещать линии относительно друг друга, и добиваясь требуемого результата.

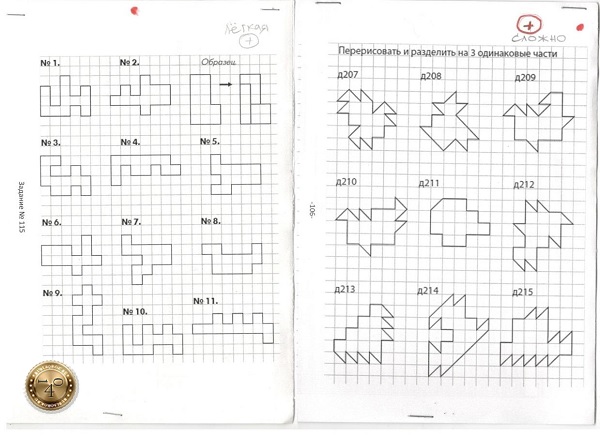
Задачи с тетрамино (№115) и, так называемые, «делилки» тоже решаются неоднозначно путем перебора множества вариантов.

1.5.2.3 Не забывай об устном счете

Устный счет развивает межполушарные связи мозга, является одним из лучших средств для тренировки памяти, воображения и интуиции. Ни один урок математики не может обходиться без устного счета. К нему полезно обсуждать условия задачи и её решение в уме.

1.5.2.4 Повторяй пройденные темы

Школьная программа построена на «прохождении» тем. Отработали конкретный параграф — перешли к другому, как говорят «галопом по Европам».

А ведь недаром говорят:

«Повторение – мать учения».

А умные люди добавляют:

«Шестикратное повторение – бабушка учения».

Если процесс возврата к ранее изученной теме сделать ещё и творческим, освещая её с разных сторон (ПРИНЦИП ОТКРЫТОСТИ), мы добиваемся эффекта, который является целью любого обучения и называется «свободное владение материалом».

1.5.2.5 Поручай сочинение задач ученикам и давай им порулить

Этот прием приветствует ТРИЗ-педагогика. Оно и понятно. Сочинение задач – это творческая деятельность, т.е. то, чему учит эта методика. Всякий тренинг в данном направлении идет на пользу дела.

Теперь о преподавании.

Есть такой старый учительский анекдот:

Жалуется педагог:

«Ну и тупые студенты пошли. Я ему объясняю, объясняю, а он не понимает! Я опять ему объясняю, объясняю, а он не понимает!! Я снова ему объясняю. Уже сам понял, а он всё не понимает!!!»

О чём здесь речь. Лучший способ усвоить материал… — начать его преподавать.

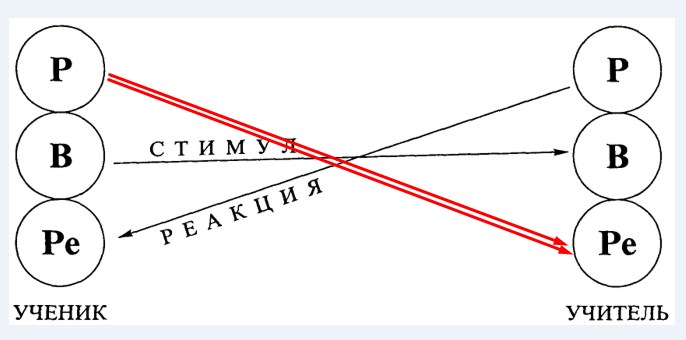
Есть и ещё один плюс. Давая задание сочинить задачу или поручая проверить чью-то работу, мы трансакцию “Дитя (ученик) – Родитель (преподаватель)” меняем на противоположную: “Родитель (ученик) — Дитя (преподаватель или другой ученик)”. Эффект потрясающий.

Проверено на моей внучке. Она категорически отказывалась решать задачки по математике. Тогда я намеренно неправильно сделал несколько наглядных задач и отдал ей на проверку со словами: «Эти задачи решили мои ученики. Помоги мне, проверь, пожалуйста». Внучка с энтузиазмом взялась за дело. Весь вечер я только и слышал: «Дед, тут неправильно! Как так можно?»

1.5.2.6 Как избавиться от привычки спешить

На дорогах «торопыг» останавливают лежачие полицейские и угроза штрафа.

В процессе обучения математике роль лежачего полицейского выполняют задачи с зашифрованным текстом:

Дачаза №1

Ростилипо вда баробнесёк. Выйпер 102 жаэат.

Ройтов – 134.

В ждамко личос втиракр ан тежэа кодинавоео.

Косколь варкрит в ждомка, слие в мосам московы

беробнесёк ан 128 равкрит шельоб?

Дачаза №2

Ан вальребу диласпио 15 родяв полотей оп 8 в

ждамак друя и кольтос еж неловк.

Вколен лобы 9 воякр, внуропо в ждокам рудя.

Косколь веклон в ждокма дуяр?

1.6 Мой типовой урок

Вооружившись методикой ТРИЗ-педагогики я разработал структуру типового урока, которую с успехом применяю в групповых занятиях.

Длительность урока 2 часа, в т.ч.

Занимательная математика – 55 минут

Физкультурная пауза — 5 минут

Шахматы — 30 минут

Великая битва (по выбору) — 30 минут

1.6.1 Занимательная математика

План урока от 22 июля 2017 г для группы на «Николиной горе»

(Тема: Устный счет, таблица умножения) – 55 минут

Начинаем с музыкальной паузы:

1)Deep Purple — Smoke On The Water 1972 (HQ) – 5 минут

Кратко рассказываю об истории написания песни, группе и исполнителях

Deep Purple

2) Разминка. Открытая задача «Не верю» из книги «Сказки-изобреталки от Кота Потряскина» — 10 минут

Сказка «Не верю»

3) ТЕОРИЯ «Как выучить таблицу умножения» – 20 минут

• Умножение на 1,10, 2, 4, на примере сложения,
• Умножение на 5, 3, 6,7,8,объясняя, что от перемены мест сомножителей произведение не меняется,
• Умножение на  9 на пальцах

Помощь : Таблица Пифагора

Обучение таблице умножения на карточках разного цвета. Ответ на обороте.

СЛОЖНЫЕ

3х4=12 3х6=18 3х7=21 3х8=24 4х7=28 4х8=32

Рифмы

6х4=24

5х5=25

6х6=36

6х8=48

Подобные

3х3=9

4х4=16

7х7=49

8х8=64

6х8=48

Умножение на пальцах на 6 7 8 9 (сайт marivana.ru)

Нумеруем пальцы.

Нумеруем пальцы от 6 до 10

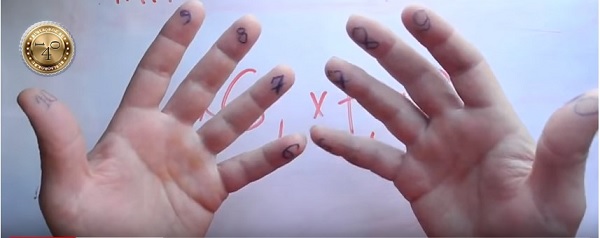
Умножаем 7 на 8. Соединяем соответствующие пальцы.

7 умножаем на 8

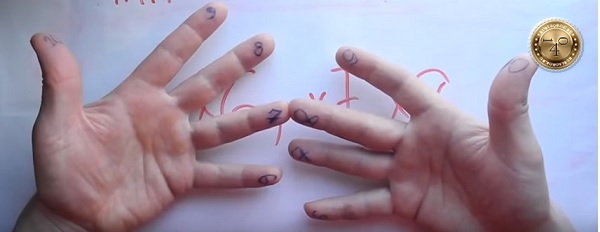
Считаем пальцы, которые снизу. Их ПЯТЬ — 50

5 пальцев снизу — 50

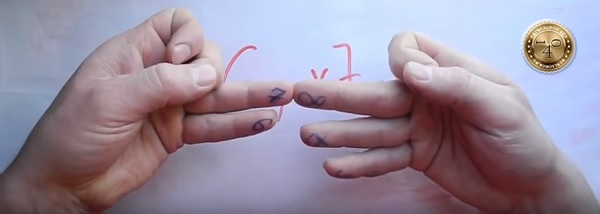
Считаем пальцы, которые сверху: 3 и 2 Три умножаем на два получаем ШЕСТЬ

3 умножаем на 2 получаем 6

Итого: 7 х 8= 50+6 = 56

4) Решаем задачу с инспектором Людовиком «Ночной вызов» – 10 минут

5) Игра «Крестики – Нолики» по таблице умножения – 10 минут

Крестики-нолики на Таблице умножения

1.6.2 Шахматы – 30 минут

1.6.3 Великая битва – 30 минут

Перед уроком вычисляем, сколько лет назад происходило сражение. В процессе рассказа считаем временные периоды, возраст исторических персонажей (скрытый устный счет)

Пример рассказа о великом сражении:

48 год до н.э. Битва при Фарсале.

«Бейте в лицо!»

Решающая битва гражданской войны между двумя римскими полководцами — Юлием Цезарем и Гнеем Помпеем «Великим». Она стала для обоих испытанием их военного искусства. Сразу несколько тактических ходов в сражении при Фарсале (со стороны как победителей, так и проигравших) заслуживают нашего внимания. Но исход дела решила оригинальная ловушка для вражеской кавалерии, которую придумал Цезарь.

Он построил центр войска так, чтобы часть легионеров задержала конницу, прорвавшуюся во фланг. А чтобы окончательно остановить напор молодых всадников, Цезарь приказал метать дротики им в лица

Красс.

После гибели Красса в 53 году до н.э. «триумвират», сформированный в 60 г. до н.э. из трех самых могущественных людей Рима (Цезарь, Помпей, Красс), распался, и оставшаяся парочка начала борьбу за власть между собой.

Марк Лици́ний Красс (лат. Marcus Licinius Crassus; 115 или 114 — май 53 гг. до н. э.)

Юлий Цезарь.

В 52 году до н.э. Юлий Цезарь в качестве проконсула (фактически — наместника) окончательно приводит к покорности Галлию, в результате этой кампании его репутация в Римской республике ощутимо выросла. Уже через год между экс-триумвирами начинается открытый конфликт.

Помпей с помощью римского сената добился того, что Цезарь должен был освободить должность проконсула. Для Цезаря это было равносильно политическому самоубийству: галльские земли приносили ему солидный доход, благодаря которому Юлий приобрёл себе в Риме так много сторонников.

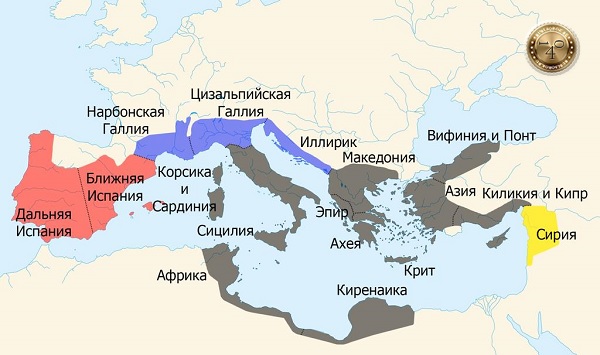
Распределение провинций между триумвирами после совещания в Лукке (завоевания Цезаря не показаны):

Цезарь: Цизальпийская Галлия, Нарбонская Галлия, Иллирик.

Помпей: Ближняя Испания, Дальняя Испания.

Красс: Сирия. Другие провинции Римской республики.

Другие провинции Римской республики.

Впрочем, Цезарю с помощью хитроумных политических интриг удалось спровоцировать Помпея первым начать военное столкновение. После нескольких стычек «Великий», которого всё тот же сенат объявил теперь вне закона, был вынужден покинуть Италию и искать поддержки у своих восточных легионов.

Основные военные действия между сторонниками обоих вождей развернулись на севере Греции. В бою при Диррахии Цезарь потерпел незначительное поражение и решил отходить в Фессалию, где стояли его резервные легионы. Но Помпей настиг соперника, и 6 июня 48 г. до н.э. у Фарсала экс-триумвиры сошлись в решающем сражении.

Гней Помпей (слева) и Юлий Цезарь

Впоследствии сам Цезарь в своих мемуарах утверждал, что силы Помпея значительно превосходили его собственные: 45 тыс. пехоты против 22 тыс., и 7 тыс. конницы против ОДНОЙ тысячи (!)

Гней решил довольно своеобразно использовать мощь своей кавалерии. Все источники сходятся в том, что конница помпеянцев (в основном — молодые аристократы из Македонии, Фракии, Каппадокии и других провинций) была почти в полном составе сосредоточена на левом фланге.

Помпей решился на такой риск, учитывая тот факт, что его правое крыло прикрывал ручей в глубокой долине. Не самая удобная местность для ответной атаки конников Цезаря, к тому же — малочисленных. Забегая вперед, скажу, что правый фланг помпеянцев действительно оставался неприступным, пока судьба сражения не решилась окончательно в пользу сторонников Цезаря. А вот на левом крыле, которое возглавил один из лучших военачальников Помпея, Лабиен, развернулись основные события — правда, вовсе не в том ключе, в каком рассчитывал «Великий».

Римская вспомогательная кавалерия

Кроме того, Гней придумал еще один остроумный прием, который мог бы склонить чашу весов в его пользу. Он рассчитывал начать сражение с атаки конницы на левом фланге и полагал, что в ответ Цезарь двинет вперед пехоту. Своим легионерам Помпей приказал оставаться на месте: цезарианцы должны были добежать до позиций врага уставшими и потерявшими строй. Но в бою эта хитрость не сработала: воины Цезаря разгадали её и попросту остановились на полпути — перевели дух, выправили строй и спокойно двинулись дальше.

Юлий Цезарь внимательно наблюдал за передвижениями противника и заметил большие массы конников, сосредоточившиеся на левом крыле Помпея. Всей конницы Юлия, состоявшей из галльских и германских всадников, не хватило бы, чтобы предотвратить прорыв помпеянцев. Можно было, например, воспользоваться хитростью Ганнибала в битве при Заме и попробовать увести кавалерию противника с поля боя, но Цезарю было известно, что флангом помпеянцев командует Лабиен — опытный полководец, который вряд ли купится на такую уловку. И Юлий придумывает свой собственный оригинальный контрприём.

Еще со времен первых легионов пехота римлян традиционно строилась в три линии. После реформ Гая Мария, как мы помним, вооружение всех легионеров было унифицировано, но принцип построения остался. Цезарь решил ограничиться двумя линиями пехоты, рассчитывая на стойкость и выучку своих легионеров.

Шесть когорт (3 тысячи человек) он поставил под углом в 90 градусов к своему правому флангу — туда, куда должен был обрушиться удар конницы Помпея (из остатков третьей линии полководец сформировал резерв).

При этом когорты получили весьма нетривиальный приказ: целиться дротиками-пилумами исключительно в лица врагов!

Я уже упоминал, что в кавалерии Помпея служили в основном молодые аристократы. Они были готовы к красивой героической смерти, но им вовсе не улыбалась перспектива вернуться к любимым дамам изуродованными на всю жизнь!

Схема битвы при Фарсале

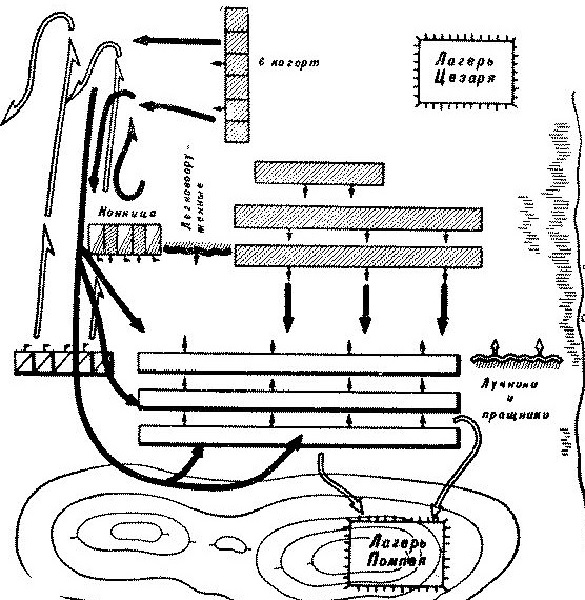
Битва началась, и пока в центре рубились пешие легионы, на левом фланге Помпея (соответственно, на правом — Цезаря) произошло следующее. Конница Цезаря не приняла боя и отступила. Лабиен не стал её преследовать, развернул кавалеристов для удара во фланг цезарианцам и… Столкнулся с тремя тысячами пехотинцев, стоявших с его всадниками лицом к лицу. Завязалась новая схватка, и пилумы, летящие в лица, привели кавалеристов в замешательство.
Пользуясь удобным моментом, галльско-германская конница Цезаря вернулась в битву и ударила Лабиену в тыл. Всадники помпеянцев попали в «мешок» и были разбиты. Дальнейшее для Цезаря являлось уже делом техники. Его правое крыло, которому больше ничто не угрожало, выдвинулось вперёд и, в свою очередь, обрушилось на Помпея с фланга, а галлы и германцы прошлись по тылам врага, разметав всю легковооруженную пехоту и стрелков.

В этот же момент на помощь центру пришел пеший резерв Цезаря.

Столкновение пеших легионов в битве при Фарсале.

К ночи остатки легионов Помпея сдались на милость победителей. Убитыми помпеянцы потеряли около 6 тысяч человек. Потери Цезаря современные историки оценивают примерно в тысячу бойцов (сам он, как водится, в мемуарах пишет лишь о двухстах).

Любопытный факт. Похожую военную хитрость применил русский князь Дмитрий Донской в знаменитой Куликовской битве 1380 года. Когда монголо-татарская конница прорвала фронт полка левой руки русских, она неожиданно наткнулась на закованную в латы тяжелую литовскую пехоту. А пока шла рубка, в тыл монголам подоспела кавалерия засадного полка.

А Гней Помпей, прославленный полководец, бежал с поля боя, бросив свои легионы: в этот раз политик в нём взял верх над воином.

Маршрут бегства Помпея

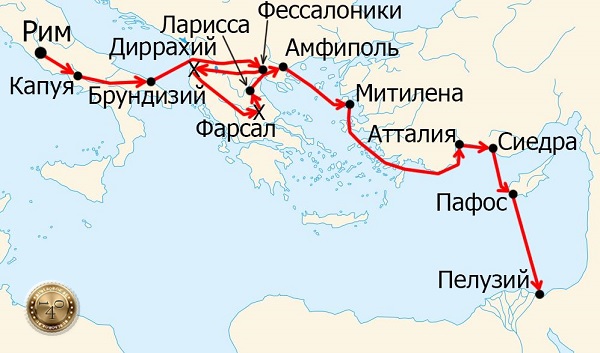
Впрочем, вскоре Гней был убит в Египте — власти этой страны не решились ссориться с могущественным Римом и его новым правителем — Цезарем. Сам же Юлий получил титул диктатора на 10 лет, и с этого момента можно говорить о том, что Римская республика превратилась в империю.

Это произошло 29 сентября 48 года до н. э. Голову Помпея и его кольцо с печатью (лев, держащий в лапе меч) египтяне преподнесли Цезарю; по преданию, он не знал о судьбе Гнея и заплакал, увидев голову. Похоронный обряд с телом Помпея провели его вольноотпущенник Филипп и один из ветеранов его армии, использовав для погребального костра обломки старой лодки. Предполагается, что пепел Помпея впоследствии был перезахоронен Корнелией Метеллой в имении Помпея в Альбоне(современный Альбано-Лациале)

Историк Аппиан, впрочем, сообщает, что могилу Помпея в Египте засыпало песком, и только император Адриан разыскал её и восстановил; о том, что тело полководца захоронено в Египте, сообщает и Страбон.

Вот вкратце и всё, что я хотел сказать на тему «Математика 1 класса без ошибок».  Как вам статья? Свои отзывы пишите в комментах.

С уважением

Автор блога Алексей Фролов